地形扭曲了方向冠层间隙率,进而影响叶面积指数实测和传感器探测到的冠层反射率。路径长度(PL)校正是一种简单、有效的坡地校正方法。对连续冠层,已有研究已对PL校正进行了严格的理论推导。然而,对于离散冠层,PL表现出严重的异质性,迫切需要发展理论推导,以评估PL校正在森林冠层中的效果。在本研究中,(1)PL校正首先被证明对具有泊松树分布的森林是完全有效的,但对于树木分布偏离泊松模型的森林,尤其是树冠分布规则的森林,可能在某些方向产生不确定性。(2)在通用森林冠层间隙率模型的基础上,提出了一种改进的森林PL校正模型。结果表明,改进后的模型能有效地降低部分PL校正在森林冠层中所产生的误差。树冠分布参数cB(θ)随坡度的变化是造成森林PL校正产生误差的主要原因。该研究对于更好地理解和更准确地应用PL理论进行山地森林冠层的地形校正和叶面积指数的野外测量具有重要意义。
研究背景:
坡地改变了冠层结构,扭曲了太阳-目标-传感器三者空间关系。路径长度(PL)校正被广泛应用于从坡地到平地的多种参数(例如冠层间隙率、反射率、叶面积指数、聚集度指数等)校正。已有研究证明,基于严格的理论推导,PL校正对于连续冠层是有效的。然而,离散的冠层(例如森林),目前仍然缺乏严格的理论推导。一个重要原因是连续冠层与离散冠层之间的PL存在明显差异(如图1所示)。本研究的目的是给出一个明确的森林PL校正推导过程。我们想要回答以下问题:(1)PL校正对于森林冠层是否完全可行?(2)如果不是,是什么原因,如何提高其精度?

模型原理:
(1)连续冠层PL校正原理回顾和PL校正本质
PL早期应用于Beer-Lambert 定理计算平地连续冠层间隙率,如公式 (1) 所示

其中,P为冠层方向间隙率,G为叶倾角投影系数,与叶倾角分布密切相关;ρ为叶面积体密度,l为PL。
对于坡地连续冠层(图2),PL可以表达为

其中,h为冠层高度;θ为观测天顶角;λ是一个非常重要的坡地校正系数,与观测天顶角θ、观测方位角φ、坡度α和坡向β密切相关(图3),可以表达为,

坡地和平地连续冠层某一方向上的PL关系本质上属于空间几何,具体证明见论文II.A推导。

综上可得,坡地和平地连续冠层的间隙率关系如下所示。换言之,只需已知观测天顶角、观测方位角、坡度和坡向四个角度信息,便可将坡地连续冠层间隙率转化为同方向的平地间隙率。

公式 (5) 是PL校正的核心。本质上,PL校正原理是冠层方向间隙率的校正。
(2)树冠随机分布下的森林PL校正证明
上述推导过程在连续冠层严格有效,然而,对于森林等离散冠层,仍需要进一步证明。树冠随机分布是遥感辐射传输模型、几何光学模型等正演模型以及反演模型中常见的假设。对于树冠随机分布下的水平森林,其冠层间隙率可以表达为:

此处n为树冠数目,ta为单棵树冠在视线主平面上的投影面积,pc为单棵树冠间隙率,SP(θ)为样地在视线主平面上的投影面积。同理,根据空间几何学,对于树冠随机分布下的坡地森林的冠层间隙率公式为:

根据空间几何可以证明(图3),这种情况下坡地和平地间隙率的关系完全满足PL校正。即对于树冠随机分布下的森林,PL完全有效(详细推导过程见论文II. B)。


(3)树冠非随机分布下的森林PL校正评估
虽然树冠随机分布在遥感辐射传输和几何光学模型以及参数反演中是常见的假设,但是真实世界的森林却不仅仅具有随机性,还表现出排斥和聚集等特性。Geng 等将泊松分布加入树冠排斥因子,构建超几何分布,推导出适合于规则分布下的森林冠层间隙率,该模型被证实在小尺度(例如10m~100m)下广泛适用 (Geng et al., 2016, 2017)。Geng 等最新研究构建了一个适合于多种树冠空间分布的森林冠层间隙率模型,发现对于多种树冠分布均具有普遍适用性,且能够同时满足平地和坡地应用 (Geng et al., 2023)。本研究基于Geng 等提出的通用森林冠层间隙率模型,推导出坡地和平地森林冠层间隙率的关系如下(详细公式推导过程见论文II.D),

该公式与公式(5)唯一的区别在于加入了树冠分布参数cB,使得模型能够适合多种树冠分布下的森林,而非局限于随机分布。从公式可以发现,坡地到平地冠层间隙率转换时,若树冠分布不变,则PL有效;若树冠分布发生变化,PL可能会产生误差。
研究方法:
研究基于(Yin et al., 2020)文中森林场景,拓展为多种分布下的场景(图4)。根据公式(5)、(8)分别计算坡地和水平森林冠层间隙率,评估PL和新模型在森林冠层中的效果。

主要结果:
以光线跟踪算法结果作为参照,发现树冠随机分布下森林冠层PL校正精度非常高;然而,当树冠偏离随机分布,PL在某些方向会产生一定误差。这是由于PL校正是基于e指数形式的校正(公式(5)),对于树冠随机分布的森林而言,坡地和平地冠层间隙率关系完全满足e指数形式。然而,对于非随机分布,这种关系并非完全成立。一个简单的例子:对于球形树冠且有明显间距的森林,若垂直于下坡方向树冠未发生重叠,该方向的冠层间隙率P’=1-n*ta*(1-pc)/SP’(θ),此处n为树冠数目,ta为单棵树冠在视线主平面上的投影面积,pc为单棵树冠间隙率,SP’(θ)为样地在视线主平面上的投影面积;若此时同方向下的平地树冠间也未发生重叠,则P=1-n*ta*(1-pc)/SP(θ)。显然,此时坡地和平地冠层间隙率并不满足公式(5)关系。
结果表明,对于树冠规则分布的森林,PL在下坡方向可能产生误差;对于聚集分布,PL在上坡会产生一定误差。改进方法能够很好地降低误差,适用于随机、规则、聚集分布下的森林冠层。

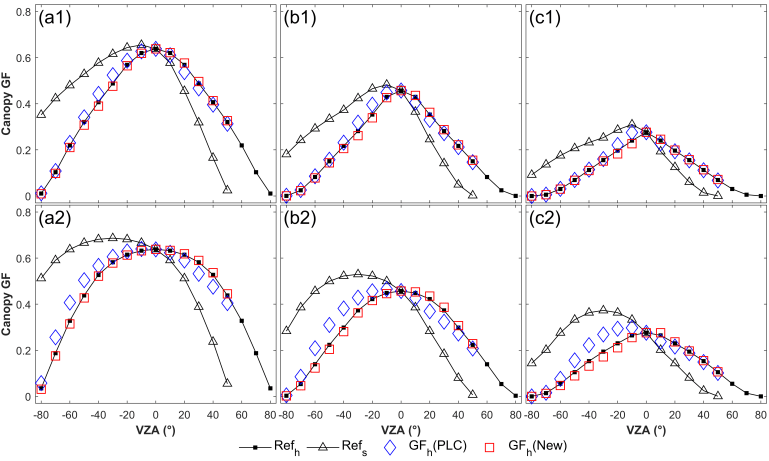

(坡地GF (a1), 平地GF (a2), PL结果(b1), 新模型结果(b2), PL误差(c1), 新模型误差(c2), PL相对误差(d1), 新模型相对误差(d2))

(坡地GF (a1), 平地GF (a2), PL结果(b1), 新模型结果(b2), PL误差(c1), 新模型误差(c2), PL相对误差(d1), 新模型相对误差(d2))
项目资助
本研究得到国家自然科学基金(41701383、41801234、4197128)、安徽省自然科学基金(2208085MD90)、中央部署高校学术新人项目(JZ2022HGTB0253)以及国家留学基金委(202006695009)项目资助。
主要参考文献
- J. Geng, Jing-M. Chen, L. Tu*, G. Yin*, H. Jin, J. Huang, J. Roujean., “Evaluation of Path Length Correction for Forest Canopies over Sloping Terrains: Theoretical Derivations and Computer Simulations,” IEEE Transactions on Geoscience and Remote Sensing, doi: 10.1109/TGRS.2023.3334681.(本研究)
- J. Geng, J. Roujean, A. Kuusk, Y. Pang, L. Tu*, Jing-M. Chen*, “A Universal Canopy Gap Fraction Model for Forests with Various Tree Distributions Based on Nilson’s Models Considering Directional Overlaps Among Crowns”. Agricultural and Forest Meteorology, Under Review. 2023. http://dx.doi.org/10.2139/ssrn.4570868.
- J. Geng,Jing-M. Chen, L. Tu, et al., “Influence of the exclusion distance among trees on gap fraction and foliage clumping index of forest plantations,” Trees, vol. 30, no. 5, pp. 1683-1693, 2016. doi:10.1007/s00468-016-1400-y.
- J. Geng, Jing-M. Chen*, L. Tu, et al., “GOFP: A Geometric-Optical Model for Forest Plantations,” IEEE Trans. Geosci. Remote Sensing, vol. 55, no. 9, pp. 5230-5241, 2017. doi:10.1109/TGRS.2017.2704079.
- G. Yin, B. Cao, J. Li, et al., “Path Length Correction for Improving Leaf Area Index Measurements Over Sloping Terrains: A Deep Analysis Through Computer Simulation,” IEEE Transactions on Geoscience & Remote Sensing, vol. 58, no. 7, pp. 4573-4589, 2020. doi:10.1109/TGRS.2019.2963366.
供稿:耿君